
Trigonometry table formulas – Trigonometry is a branch of mathematics which includes the analysis of the relationship between a triangle’s length and angles. In general, it is aligned with a right-angled triangle, where 90 degrees is always one of the angles. In other areas of mathematics, it has a large range of applications. Using the table of trigonometric functions and formulas, certain geometric equations can also be quickly found out.
Read more: Essay on Gender Equality
Trigonometric identities are formulas that involve Trigonometric functions. These identities are true for all values of the variables. Trigonometric Ratio is known for the relationship between the measurement of the angles and the length of the sides of the right triangle.
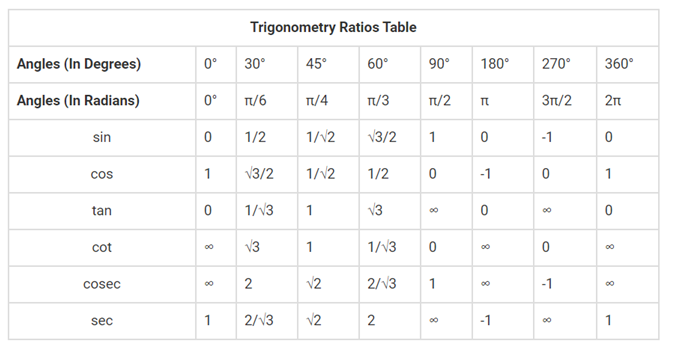
The table of trigonometric ratios helps locate the values of regular trigonometric angles, such as 0 ° , 30 °, 45 °, 60 ° and 90 °. The values of regular angle trigonometric ratios are sufficient to solve the problems of trigonometry. The values of the trigonometric ratios of these regular angles must, however, be remembered.
Trigonometric functions
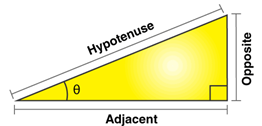
| Functions | Abbreviation | Relationship to sides of a right triangle |
| Sine Function | sin | Opposite side/ Hypotenuse |
| Tangent Function | tan | Opposite side / Adjacent side |
| Cosine Function | cos | Adjacent side / Hypotenuse |
| Cosecant Function | cosec | Hypotenuse / Opposite side |
| Secant Function | sec | Hypotenuse / Adjacent side |
| Cotangent Function | cot | Adjacent side / Opposite side |
Trigonometry ratio table
Trigonometry formulae to remember
- sin x = cos (90° – x)
- cos x = sin (90° – x)
- tan x = cot (90° – x)
- cot x = tan (90° – x)
- sec x = cosec (90° – x)
- cosec x = sec (90° – x)
- 1 / sin x = cosec x
- 1/ cos x = sec x
- 1/ tan x = cot x
Pythagorean identities
- sin² θ + cos² θ = 1
- tan2 θ + 1 = sec2 θ
- cot2 θ + 1 = cosec2 θ
- sin 2 θ = 2 sin θ cos θ
- cos 2 θ = cos² θ – sin² θ
- tan 2 θ = 2 tan θ / (1 – tan² θ)
- cot 2 θ = (cot² θ – 1) / 2 cot θ
Co-function identities
- sin (90°-x) = cos x
- cos (90° -x) = sin x
- tan (90° -x) = cot x
- cot (90° -x) = tan x
- sec (90° -x) = cosec x
- cosec (90° -x) = sec x
Sum and difference identities
- sin (x+y) = sin (x) cos (y) + cos (x) sin (y)
- cos (x+y) = cos (x) cos (y) – sin (x) sin (y)
- tan (x+y) = (tan x + tan y)/ (1−tan x • tan y)
- sin (x–y) = sin (x) cos (y) – cos (x) sin (y)
- cos (x–y) = cos (x) cos (y) + sin (x) sin (y)
- tan (x−y) = (tan x–tan y)/ (1+tan x • tan y)
Half Angle identities
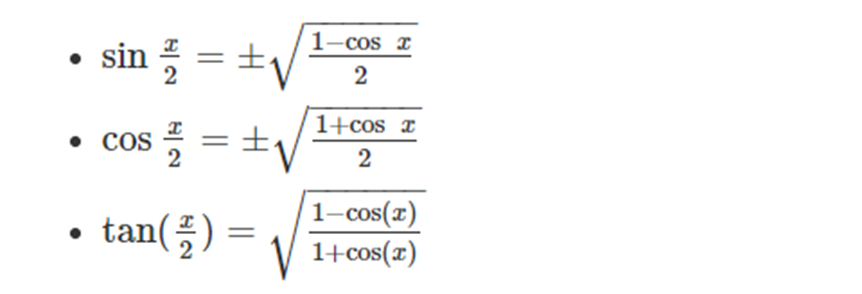
Product identities
- sin x ⋅ cos y = sin (x+y) + sin (x−y) /2
- cos x ⋅ cos y = cos (x+y) + cos (x−y) /2
- sin x ⋅ sin y = cos (x−y) − cos (x+y) /2
Inverse formulae
- sin-1 (–x) = – sin-1 x
- cos-1 (–x) = π – sin-1 x
- tan-1 (–x) = – tan-1 x
- cosec-1 (–x) = – cosec-1 x
- sec-1 (–x) = π – sec-1 x
- cot-1 (–x) = π – cot-1 x
How to solve trigonometric questions
If we have been given with height of the building and the angle formed when an object is seen from the top of the building, then the distance between object and bottom of the building can be determined by using the tangent function, such as tan of angle is equal to the ratio of the height of the building and the distance. Let us say the angle is ∝, then
Tan ∝ = Height/Distance between object & building
Distance = Height/Tan ∝
Let us assume that height is 20m and the angle formed is 45 degrees, then
Distance = 20/Tan 45°
Since, tan 45° = 1
So, Distance = 20 m
Problems with solutions – Trigonometry table
These problems can be solved with the help of the formulae provided above.
- A started climbing a pyramid-shaped hill. A climbs 315 m and finds that the angle of depression is 72.3 degrees from his starting point. How high is he from the ground?
Solution
Let m be the height that needs to be found
Therefore, Sin 72.3° = m/315
0.953 = m/315
m= 315 x 0.953
m=300.195 mtr
A is 300.195 mtr above the ground.
2. A man is observing a pole of height 55 foot. According to his measurement, the pole cast a 23 feet long shadow. What is the angle of elevation of the sun from the tip of shadow?
Solution:
Let m be the elevation of the sun
Therefore, tan m = 55/23 = 2.391
m = tan-1(2.391)
or m = 67.30 degrees
The angle of elevation of the sun from the tip of the shadow is 67.30 degrees.
Prove
3. sec θ √(1 – sin2 θ) = 1
Solution
Let A = sec θ √(1 – sin2 θ) and B = 1.
A = sec θ √(1 – sin2 θ)
Because sin2 θ + cos2 θ = 1, we have
cos2 θ = 1 – sin2 θ
Then,
A = sec θ √cos2θ
= sec θ ⋅ cos θ
A = sec θ ⋅ (1/ sec θ)
= sec θ / sec θ
A = 1
A = B (Proved)
4. Prove : tan4 θ + tan2 θ = sec4 θ – sec2 θ
Solution
Let A = tan4θ + tan2θ and B = sec4θ + sec2θ.
A = tan4θ + tan2θ
A = tan2θ (tan2θ + 1)
We know that,
tan2θ = sec2θ – 1
tan2θ + 1 = sec2θ
Then,
A = (sec2θ – 1)(sec2θ)
= sec4θ – sec2θ
A = B (Proved)
5. Calculate the length of the side x, given that tan θ = 0.4
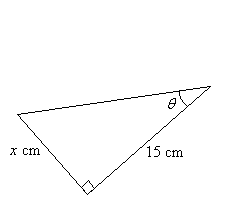
Solution
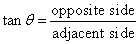
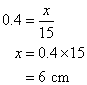
6. Prove: (1 – sin A)/ (1 + sin A) = (sec A – tan A)2
Solution:
L.H.S = (1 – sin A)/(1 + sin A)
= (1 – sin A)2/(1 – sin A) (1 + sin A), ………. Multiply both numerator and denominator by (1 – sin A)
(1 – sin A)2/(1 – sin2 A)
= (1 – sin A)2/(cos2 A), [Since sin2 θ + cos2 θ = 1 ⇒ cos2 θ = 1 – sin2 θ]
{(1 – sin A)/cos A}2
= (1/cos A – sin A/cos A)2
= (sec A – tan A)2 = R.H.S. Proved.
Similarly, many more examples can be solved with the help of these formulae
Conclusion
Trigonometry table formulas for class 11 and 10 – From the examples and the formulae provided above, we will be able to solve derivations as well as word problems. One of the most important real-life applications of trigonometry is in the calculation of height and distance. It is important to remember the trigonometry table as it is forms our basics of trigonometry